Design Project 1 (wheeled cat-catching robot)
- System
- Model
- Tasks
- Deliverables
- Draft report with theory (by 11:59pm on Friday, February 7)
- Draft report with results (by 11:59pm on Friday, February 14)
- Final report (by 11:59pm on Friday, February 21)
- Final video (by 11:59pm on Friday, February 21)
- Final code (by 11:59pm on Friday, February 21)
- Individual reflection (by 11:59pm on Monday, February 24)
- Evaluation
System
The first project that you will complete this semester is to design, implement, and test a controller that enables a wheeled robot to balance upright and to catch test-pilots (cats) who have been hired to evaluate a prototype launch system.
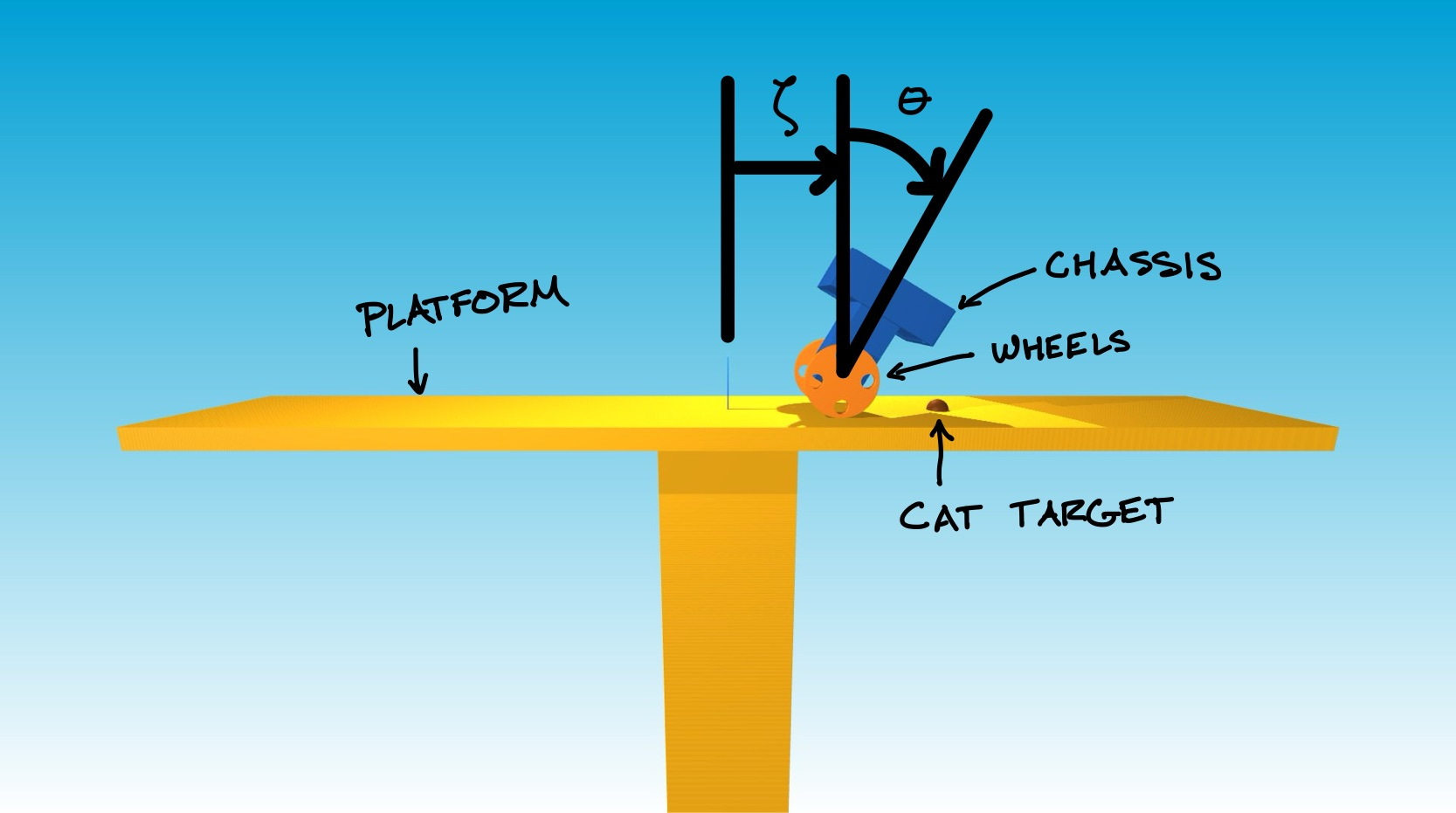
The robot consists of a chassis (dark blue) and of wheels (orange). This sort of robot is often called “differential-drive” because two separate motors allow a different torque to be applied by the chassis to the left wheel and the right wheel, and so allow the robot to turn one way or the other.
A differential-drive transmission is a common design choice for mobile robots. For example, NASA used it in a prototype of Robonaut. You can read more about the reasons why in the textbook Introduction to Autonomous Mobile Robots, Second Edition (Siegward, Nourbakhsh, and Scaramuzza, 2011), also available online (for free from the library at Illinois and at other academic institutions). The two-wheeled, differential-drive design has also been popularized by consumer products like the Segway Ninebot S2 or the Segway RMP.
In this project, you will focus only on motion forward and backward and will assume that the same torque is applied to both wheels.
The launch system uses a catapult to throw pilots at high velocity from the ground to an elevated platform (yellow). This launch system is designed so that the pilots follow a parabolic trajectory to arrive at a much lower velocity just above the platform. This low velocity is chosen so that pilots will be safe if they are caught (and held without dropping) in the basket carried on top of the robot.
This launch system is unable to make each pilot land at the same place on the platform, unfortunately. However, it is able to quickly and accurately predict the target (red sphere) where each pilot will land, shortly after launch.
Cats have been hired as pilots to test this launch system. They understand the risk and are eager to fly. Your job is to keep them safe.
Model
If we assume that the wheels roll without slipping on the surface of the platform, then the motion of the robot is governed by ordinary differential equations with the form
\[M(q) \ddot{q} + N(q, \dot{q}) = F(q) r\]where
\[\begin{gather*} M(q) = \left[\begin{matrix}(J_{w} / r_{w}^{2}) + m_{b} + m_{w} & m_{b} r_{b} \cos{\left(\theta \right)}\\m_{b} r_{b} \cos{\left(\theta \right)} & J_{b} + m_{b} r_{b}^{2}\end{matrix}\right] \\ N(q, \dot{q}) = \left[\begin{matrix}- m_{b} r_{b} \sin{\left(\theta \right)} \dot{\theta}^{2}\\- g m_{b} r_{b} \sin{\left(\theta \right)}\end{matrix}\right] \\ F(q) = \left[\begin{matrix}1 / r_{w}\\-1\end{matrix}\right] \end{gather*}\]and
\[q = \begin{bmatrix} \zeta \\ \theta \end{bmatrix} \qquad\qquad r = \begin{bmatrix} \tau \end{bmatrix}.\]The variables in these equations are defined as follows:
- $\zeta$ is the wheel position ($\text{m}$);
- $\dot{\zeta}$ is the wheel velocity ($\text{m}/\text{s}$);
- $\theta$ is the pitch angle ($\text{rad}$) — positive means tilting forward;
- $\dot{\theta}$ is the pitch rate ($\text{rad}/\text{s}$);
- $\tau$ is the wheel torque ($\text{N}\cdot\text{m}$) applied by the chassis to the wheels — positive will cause the wheels to rotate forward.
The constant parameters in these equations are defined as follows:
\[\begin{align*}r_w &= 0.325 \\ m_w &= 2.4 \\ J_w &= 0.12675 \\ r_b &= 0.3 \\ m_b &= 12.0 \\ J_b &= 0.8 \\ g &= 9.81. \end{align*}\]Sensors provide measurements of the wheel position, wheel velocity, pitch angle, and pitch rate, as well as of the position that the launched cat-pilot is expected to land, i.e., the cat target ($\text{m}$), which varies up to a maximum of $\pm 2.5\;\text{m}$ from the center of the platform. Actuators allow you to choose what torque will be applied to the wheels, up to a maximum of $\pm 5\;\text{N}\cdot\text{m}$.
The code provided here simulates the motion of this system (CatbotDemo) and also derives the equations of motion in symbolic form (DeriveEOM).
Tasks
Please do the following things:
- Choose a wheel position that you want to achieve.
- Linearize the model about an equilibrium point that corresponds to this wheel position and express the result in state-space form.
- Design a linear state feedback controller and verify that the closed-loop system is asymptotically stable in theory.
- Implement this controller and verify that the closed-loop system is asymptotically stable in simulation, at least when initial conditions are close to equilibrium.
- Test the resulting launch system in simulation and verify that the robot (with your controller) is capable of catching pilots with high probability.
In doing these things, keep your focus on the safety of your pilots.
Would you feel comfortable asking a cat-pilot to test your launch system based on evidence from only one simulation (starting from only one set of initial conditions) that your controller “works”?
Would you feel comfortable asking other cats — those who are not test-pilots — to use your launch system based on the success of only a single launch?
Think carefully about what results would support a comprehensive argument for the safety of your launch system and — since no launch system is 100% reliable — try hard to identify the conditions under which failures are likely to occur.
Deliverables
Draft report with theory (by 11:59pm on Friday, February 7)
Submit a first draft of your report (see below for guidelines). This draft must include a complete Theory section, which is what we will focus on in our review. This draft must also include the Abstract, Nomenclature, and Introduction.
Upload it to the DP1 Draft 1 group assignment on Canvas.
Draft report with results (by 11:59pm on Friday, February 14)
Submit a second draft of your report (see below for guidelines). This draft must include a complete Experimental methods section and a complete Results and discussion section, which are what we will focus on in our review. This draft must also include the Conclusion, Appendix, Acknowledgements, and References.
Upload it to the DP1 Draft 2 group assignment on Canvas.
Final report (by 11:59pm on Friday, February 21)
This report will satisfy the following requirements:
- It must be a single PDF document that conforms to the guidelines for Preparation of Papers for AIAA Technical Conferences. In particular, you must use either the Word or LaTeX manuscript template.
- It must have a descriptive title that begins with “DP1” (e.g., “DP1: Control of a wheeled robot”).
- It must have a list of author names and affiliations.
- It must contain the following sections:
- Abstract. Summarize your entire report in one short paragraph.
- Nomenclature. List all symbols used in your report, with units.
- Introduction. Prepare the reader to understand the rest of your report and how it fits within a broader context.
- Theory. Derive a model and do control design.
- Experimental methods. Describe the experiments you performed in simulation in enough detail that they could be understood and repeated by a colleague.
- Results and discussion. Show the results of your experiments in simulation (e.g., with plots and tables) and discuss the extent to which they validate your control design and support an argument for the safety of your launch system.
- Conclusion. Summarize key conclusions and identify ways that others could improve or build upon your work.
- Appendix. Provide a review of your launch system from the perspective of one or more of your cat-pilots. They are important stakeholders. (How did they feel during launch? Were they involved in any accidents? Do they have concerns about launch safety? Etc.) You are welcome to refer to this appendix — i.e., to the remarks from your cat-pilots — in other parts of your report, if it is helpful in supporting your arguments.
- Acknowledgements. Thank anyone outside your group with whom you discussed this project and clearly describe what you are thanking them for.
- References. Cite any sources, including the work of your colleagues.
- It must contain a URL (with hyperlink) to your final video.
- It must be a maximum of 6 pages.
Submit your report by uploading it to the DP1 Report group assignment on Canvas.
Final video (by 11:59pm on Friday, February 21)
This video will satisfy the following requirements:
- It must be 60 seconds in length.
- The first and last 5 seconds must include text with a descriptive title (the same title as your report), your names, and the following words somewhere in some order:
- AE353: Aerospace Control Systems
- Spring 2025
- Department of Aerospace Engineering
- University of Illinois at Urbana-Champaign
- The middle 50 seconds must communicate the highlights of your methods and results to potential stakeholders. Who are you designing for? How will your controller help them?
- It must show at least one simulation of your working control system.
- It must include at least one remark from a cat-pilot.
- It must be engaging (have fun with this).
- It must not be offensive — use common sense and ask if you are uncertain.
Submit your video by uploading it to the AE353 (Spring 2025) Project Videos channel on Illinois Media Space. Please take care to do the following:
- Use the same descriptive title as your report, appended with your names in parentheses — for example, “DP1: Control of a wheeled robot (Tim Bretl and Jacob Kraft)”.
- Add the tag
dp1(a lower case “dp” followed by the number “1”), so viewers can filter by project number. - Ask someone else to confirm that they can view the video on Media Space (i.e., that it has, indeed, been published to the correct channel).
You are welcome to resubmit your video at any time before the deadline. To do so, please “Edit” your existing video and then do “Replace Media”. Please do not create a whole new submission.
We realize that 60 seconds is short! Think carefully about what to include (what to show and what to say) and anticipate the need for multiple “takes” and for time spent editing.
Please also submit the URL for your video to the DP1 Video group assignment on Canvas. You can find this URL by viewing your video on Media Space and then by clicking “Share” and “Link to Media Page”.
Final code (by 11:59pm on Friday, February 21)
This code will satisfy the following requirements:
- It must be a single jupyter notebook (with the extension
.ipynb) that, if placed in theprojects/01_catbotdirectory and run from start to finish, would reproduce all of the results that you show in your report. - It must not rely on any dependencies other than those associated with the
ae353conda environment. - It must be organized and clearly documented, with a mix of markdown cells and inline comments.
Submit your code by uploading it to the DP1 Code group assignment on Canvas. You will be asked to upload it in two formats — as the original .ipynb (so we can run your code) and as rendered .html (so we can see and comment on your code in Canvas). Follow these instructions to get your notebook in .html format.
Individual reflection (by 11:59pm on Monday, February 24)
Complete the DP1 Reflection assignment on Canvas sometime between 11:00am on Friday, February 21 and 11:59pm on Monday, February 24. This assignment, which should take no more than 10 or 15 minutes, will give you a chance to reflect on your experiences during this project and to identify things you may want to change for the next project.
Evaluation
Your project grade will be weighted as follows:
- (10%) Draft report with theory
- (10%) Draft report with results
- (40%) Final report
- (20%) Final video
- (10%) Final code
- (10%) Individual reflection
Rubrics will be discussed in class.